With the latest Windows Server 2022 cumulative update (June 2022), you are also able to run WSL 2 on Windows Server. In this blog post, I am going to show you how you can install the Windows Subsystem for Linux 2 (WSL 2) on Windows Server. The Windows Subsystem for Linux was already available in earlier versions of Windows Server; however, WSL 2 brings a lot of new advantages. WSL 2 will be available on Windows Server 2022 broadly with the June cumulative update and if you want to run it today, you can install the 5C update here.
The Windows Subsystem for Linux was in Windows 10 and Windows 11 for a while now and allowed you to use different versions of Linux on your Windows client machine. With WSL 2, the architecture will change drastically and will bring increased file system performance and full system call compatibility. WSL 2 is now using virtualization technology (based on Hyper-V) and uses a lightweight utility VM on a real Linux kernel. You can find out more about WSL 2 in the release blog or on the Microsoft Docs Page for WSL 2.
Install Windows Subsystem for Linux 2 (WSL 2) on Windows Server
Here is how you can install WSL 2 on Windows Server.
Prerequisites:
- Windows Server 2022 June cumulative update or 5c preview update (May)
- A machine that supports Hyper-V Virtualization.
- If you are installing your Windows Server in a virtual machine, make sure Nested Virtualization is enabled.
After you have installed Windows Server 2022 with the latest update, you will need to add the following features:
- Microsoft-Windows-Subsystem-Linux
- VirtualMachinePlatform
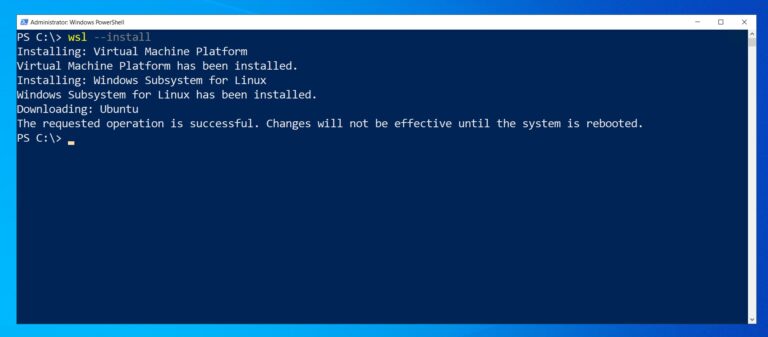
To enable these features, run the following command:
wsl --installThis command will need a restart to complete.
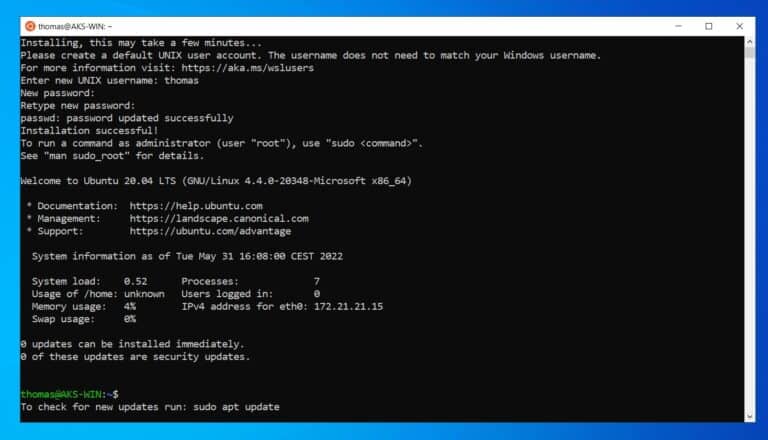
This will also download Ubuntu as for your WSL 2 Linux distro.
I hope this gives you a step-by-step guide on how you can install WSL 2 on Windows Server. If you want to install the Windows Subsystem for Linux (1( on Windows Server 2019, check out this blog post: Install Windows Subsystem for Linux on Windows Server.
Tags: Hyper-V, install, installation, Microsoft, Windows Server, Windows Server 2019, Windows Server Insider Preview, Windows Subsystem for Linux 2, Windows Subystem for Linux, WSL, WSL 2, WSL 2 on Windows Server, WSL on Windows Server Last modified: May 31, 2022
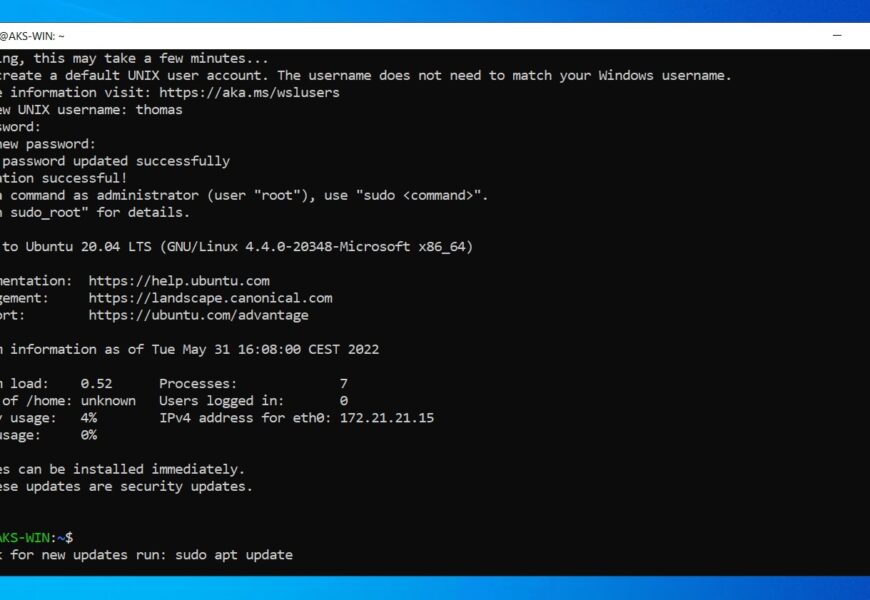









Ignore my previous comment. Figured it out.
PS C:\Windows\system32> wsl –set-version Ubuntu-18.04 2
Conversion in progress, this may take a few minutes…
For information on key differences with WSL 2 please visit https://aka.ms/wsl2
Conversion complete.
PS C:\Windows\system32> wsl -l -v
NAME STATE VERSION
* Ubuntu-18.04 Stopped 2
Great that it worked! :)
Very cool information and simple walkthrough. FYI, 2 small typos in your shell scripts above referencing Ubuntu1894 instead of Ubuntu1804.
Thanks :) and thanks for letting me know about the typos. They should be fixed now :)
I cannot set wsl to version 2. Seems several options are not available. My wsl output is:
PS C:\Users\Administrator> wsl –set-version Ubuntu-20.04 2
Invalid command line option: –set-version
Usage: wsl.exe [option] …
Options:
-d, –distribution
Launch the specified distribition.
-e, –exec
Execute the specified Linux command. The remainder of the arguments are
used as the command line to execute.
-u, –user
Run as the specified user.
–help
Display this usage information.
—
Stop parsing arguments and pass the remainder to the Linux process.
OR
PS C:\Users\Administrator> wsl –set-default-version
Invalid command line option: –set-default-version
Usage: wsl.exe [option] …
Options:
-d, –distribution
Launch the specified distribition.
-e, –exec
Execute the specified Linux command. The remainder of the arguments are
used as the command line to execute.
-u, –user
Run as the specified user.
–help
Display this usage information.
—
Stop parsing arguments and pass the remainder to the Linux process.
Hi Marcelo
Which version of Windows 10 are you running?
hi, Thomas,
how can I install WSL2 on my Windows Server 2019?
Thanks.
Bose
Hi Thomas,
Thanks for the great blog! I was wondering if it would be possible to enable Docker to run Linux containers on Server insider (20215) with WSL2? I have been searching everywhere, but all tutorials are outdated on this.
Thanks,
Janjaap
Hi, might want to correct this article for those who are misled by it’s title. This is NOT for running WSL 2 on Windows Server, this is currently not possible. It’s for running WSL 2 on Windows 10.
You are wrong :) It is for running it on Windows Server. There is another post (see the link) for Windows 10.
I get the same response to wsl.exe commands not supporting the arguments in these instructions.
Running Windows Server 2019 Datacenter version 1809 build 17763.1637.
It’s running as a E Series V3 system on Azure.
I could not get this to run on any build of Windows Server 2019 following your directions – any thoughts? Similar to others I just get the WSL output of the various WSL options.
It doesn’t work with Windows Server 2019. You need “Windows Server Insider Preview build 18945 or higher”
Just a note for those who are trying now on Windows Server Preview (actual build 20287).
The WSL2 bits are broken from build 20251 onward.
Look here to download the last build where WSL2 works and don’t do an in-place upgrade.
https://techcommunity.microsoft.com/t5/windows-server-insiders/wsl-2-not-working-after-installing-20262/m-p/2109063/highlight/true?WT.mc_id=modinfra-0000-thmaure#M1601
Any news on this Thomas? What about Windows Server 2022?
Hi Thomas,
it would be a nice utopie – but in the actual WindowsServer2022 (v21H2, build 20348.202) – WSL2 seems not supported anymore. The so far well known ‘wsl –set-default-version 2’ run without any error nor effect – it sticks at WSL1. See that comment here: https://github.com/microsoft/WSL/issues/6301#issuecomment-858816891
That is a real pity, not only for your well explaining blog post. Can you confirm this?
Not working on Azure Windows server 2022